第 16 届中国东南地区数学奥林匹克主试委员会成员 ： 熊斌 、 何忆捷 （ 华东师范大学 ） ， 李胜宏 、 杨晓鸣 （ 浙江大学 ） ， 柳彬 （ 北京大学 ） ， 李铁城 （ 清华大学 ） ， 吴泉水 （ 复旦大学 ） ， 罗晔 （ 香港大学 ） ， 张鹏程 （ 福建师范大学 ） ， 董秋仙 （ 南昌大学 ） ， 吴根秀 （ 江西师范大学 ） ， 陶平生 （ 江西科技师范大学 ）

高一年级

1. 求最大的实数k,使得对于任意的正数a 、 b, 均有

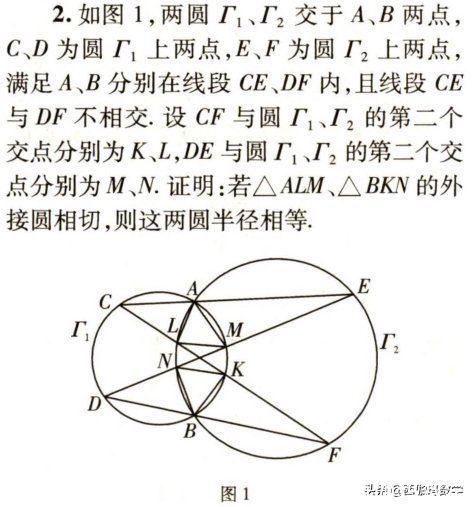
张鹏程供题

4. 将一个 2 x 5 的方格表先按照水平方向或竖直方向放置 ， 再去掉其四个角上的任意一格 ， 剩下由 9 个格组成的八种不同图形皆称为 “ 五四旌旗 ” 或 “ 八一旌旗 ” ， 简称 “ 旌旗 ” ， 如图 2 所示.

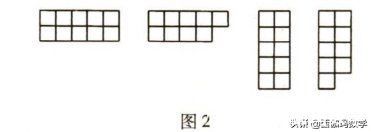
现有一个固定放置的 9 X 18 的方格表.若用 18 面上述旌旗将其完全覆盖 ， 共有多少种不同的覆盖方案?说明理由.

5. 称集合 S= |1 928,1 929,-,1 949} 的一个子集 M 为 “ 红色的 ” 当且仅当 M 中任意两个不同元素之和均不被 4 整除.用x,y分别表示 S 的红色四元子集 、 红色五元子集的个数.试比较x,y的大小 ， 并说明理由. (杨晓鸣 供题)

6 . 已知 a 、 b 、 c 为给定的三角形的三边长.若正实数 x 、 y 、 z 满足 x + y + z = 1 , 求

axy + + byz + + czx 的最大值. （ 李胜宏 供题)

文章来源：《应用数学学报》 网址: http://www.yysxxbzz.cn/zonghexinwen/2021/1028/1334.html