我们需要的最后一个术语是子簇。你们可以想象，X的一个子簇是由多项式方程零点集给出的一个子集，因此也是一个簇。

这是使霍奇猜想有趣的关键思想：从拓扑学家的观点来看，实际上没有什么多样性。

作为多项式集合的零集是非常有限的。拓扑上的东西可能会很疯狂，很奇怪且很晦涩。如果你从X的一个子簇开始，然后像我们上面做的那样对它进行任意变形，你最终得到的将不再是一个子簇。

另外，请注意，一个子簇是通过取多项式零点集并与X相交而形成的。这本质上是一个“全局”的东西。拓扑上变形的形状在某种意义上是一个“局部”的东西。

所以如果这两个不同的数学分支之间有很好的联系，我们应该感到惊讶。

霍奇猜想

在这一点上，我们可以给出的霍奇猜想最简单的表述是：

在

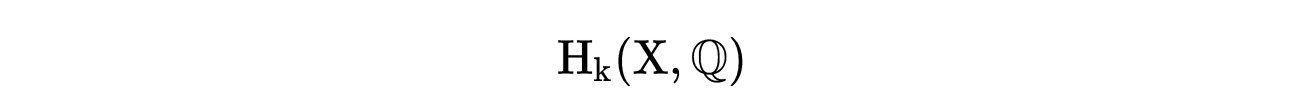
中，给定某个环[A]，是否存在一个k维子簇Y来表示[A]？我们称这样的子簇为[A]的代数代表。

让我们把它解剖一下。回想一下，A可能是奇形怪状的，它是一种基本的拓扑结构，绕着x中的一个孔。

有没有办法把A“变形”成一个由多项式方程定义的“漂亮”形状？

如果你认为答案显然是肯定的，那么你可能没有领会到作为一个子簇是多么强大和受限。如果你认为答案显然是否定的，那么你可能无法理解在不改变A的类的情况下，我们可以做多少变形。

记住，我们在复数上面，所以每个子簇都是偶维的。例如，这意味着

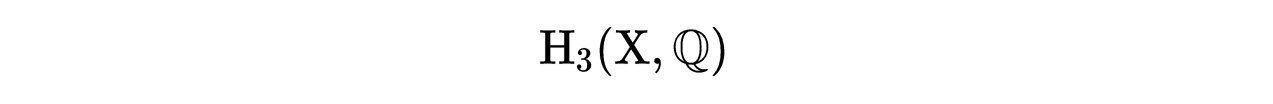
中没有代数代表。

但即使我们把自己限制在维度上，还有一个技术条件会带来问题。

如果你查霍奇猜想，标准的表述方式涉及上同调而不是同调，所以只有上标，没有下标。事实证明这些只是对偶概念。如果X有（实）维度n，那么我们可以把H?(X，?)中的[A]看作是H(X, ?)中的一个类。

这样做的原因之一是上同调可以用微分形式来解释。这意味着我们可以用积分来进行数值计算。

在我们对X的假设下，上同调有一个很好的分解，叫做霍奇分解。它甚至使用调和函数。以4为例：

一个使用一些技术机制的相当简单的计算表明，任何子簇[Y]必须落在中间的那块上。换句话说，每个子簇都是一个霍奇类。

例如，如果X是6维的（复数意义上的），而Y是二维的子簇，则[Y]属于 H?(X, ?)的(4,4)部分。

如果所有这些都有点多，就把这看作必须满足的一个额外的“数字条件”。因为每个子簇都是霍奇类，我们知道霍奇猜想的简单表述版本是不正确的，因为我们只取一个非零的非霍奇类。

霍奇猜想的正确版本是：每一个霍奇类都是代数的。换句话说，我们可以选任何一个霍奇的类，不管它有多怪异，我们都可以把它变形成一个子簇。

一些进展

事实证明霍奇猜想在低维空间中是正确的。这是由Lefschetz在1924年证明的，而霍奇猜想是1950年提出来的。在过去的几年里，也有一些其他的维度被证明，但都是在非常强大的额外假设下。

你可以想象有人做了一个天真的猜想，然后有人指出实际上子簇都是霍奇类。然后有人说，我想知道是不是所有的霍奇类都是代数的。

然后在1961年，Atiyah和Hirzebruch证明了积分版本是错误的。于是人们说，我想知道我们是否可以用Q代替Z，如果这是真的。这就是我们今天所处的处境。

与黎曼假说不同，霍奇猜想似乎是一项正在进行中的工作，在经过几次改进后陷入了困境。我们甚至不知道当X是4维且由一个多项式方程给出时它是否成立。

文章来源：《应用数学学报》 网址: http://www.yysxxbzz.cn/zonghexinwen/2021/0513/716.html