高中数学导数放缩6大题型总结,方法使用,零基
【作 者】:网站采编
【关键词】:
【摘 要】:高中数学中,导数大题总的来说只有两大类:零点问题和恒成立问题。又有很多小类:双变量赋值、极值点偏移、双切线放缩同构、凹凸性反转等。成绩想要达到120分以上,不光要掌握
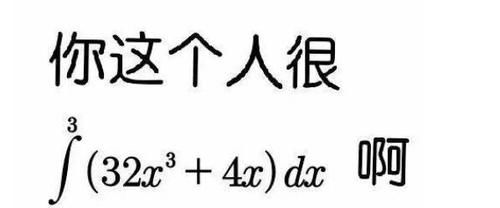









高中数学中,导数大题总的来说只有两大类:零点问题和恒成立问题。又有很多小类:双变量赋值、极值点偏移、双切线放缩同构、凹凸性反转等。成绩想要达到120分以上,不光要掌握这些题型,还要掌握实用的方法和技巧。
因为解决每一种题型,又有各种办法。放缩取点、变换主元、端点效应等。可是以上这些方法,都是建立在大量刷题、总结方法的前提上。
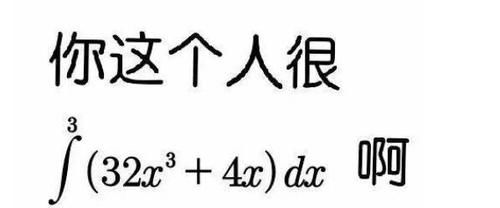
如果你没有时间做题也没有关系,因为之前的学长学姐们已经给大家整理好了。这些经验和技巧可以让你少走弯路,快速找到解题思路。解决问题,考场得分。
今天跟大家分享的是《高中数学导数放缩6大题型总结》。做选择题和填空题时,这是秒杀技巧,做大题时,这是快速解题的思路来源。(我把资料部分截图放在下面,想要这份资料提升成绩的同学,可以私下发消息给我,我安排助教老师接待大家,暗号【数学】)。









同学们有没有想过为什么要努力?我见过最好的回答就是:因为我喜欢的东西都很贵,我想去的地方都很远,我爱的人超完美。
文章来源:《应用数学学报》 网址: http://www.yysxxbzz.cn/zonghexinwen/2021/0502/669.html