大家好，本文和大家分享一道全国初中数学联赛决赛的题目。题目是一道解双根号的方程，看似非常简单，但是据说当年正确率不到10％，快来看看你是否会做呢(题目见下图)？

这是是一道解双根号方程的题目，而且都是二次根式。在初中阶段，二次根式一般是指形如√a的式子，其中a为非负数，叫被开方数。二次根式最重要的性质是具有双重非负性，即被开方数为非负数，二次根式本身的值也是一个非负数。

解双根号的二次根式方程，初中阶段常用的方法有两种：平方法和换元法。我们先来看一下下面一个简单的例子(如下图)。

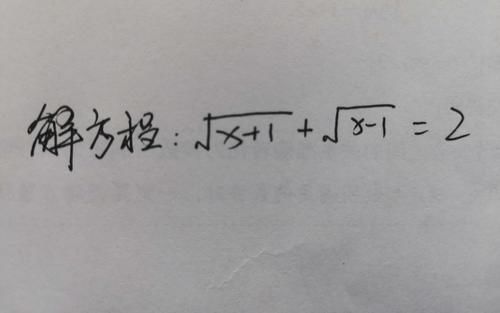
这就是一个很简单但是又很典型的双根号方程问题。下面详细讲解平方法和换元法求解的过程。

用平方法求解时，我们先将两个根号分别移动到等号的两边，而不是直接平方，这样做的目的是为了减少后面的计算量。如果有兴趣你也可以直接平方计算一次，然后进行对比，就会发现这种处理的好处了。具体过程见下图。

先将两个根号分别令为a和b，那么就有a+b=2；然后观察两个被开方数的特征，可以发现两个被开方数之差为2，即a2-b2也等于2，再用平方差公式进行分解就可以得到a-b=1。联立即可求出a和b，然后反解出x。具体过程见下图。

不管是平方法还是换元法，解出x后要进行检验，保证根式有意义。当然，也可以先根据根式有意义求出x的范围。

我们再回到这道竞赛题。这道题如果用平方法，那么计算量将会非常大，甚至会出现4次方的形式，因为方程的右边出现了x，所以平方法不太适合。下面我们再来看一下换元法。

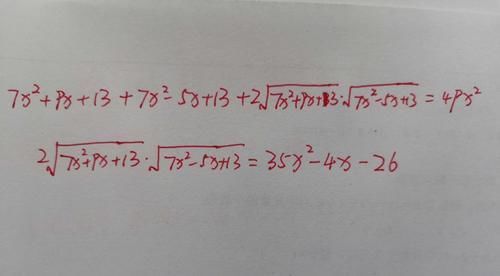
同样，先令2个根式分别为a和b，再观察被开方数的形式，可以发现两个被开方数之差为14x，于是得到a、b的方程组，先解出a、b，再代入反解x。详细过程见下图。

从上面的解题过程来看，此题实际上并不难，但是和平时做的题不一样的地方在于：平时的题a和b解出来一般是一个具体的数，而此题却含有x，导致一些同学不敢继续往下算。

下面我们再讲另外一种方法：分子有理化。

先将方程的分母看成“1”，然后进行分子有理化，这样可以得到两个根式之差的值，并且方程的右边是一个纯数字。这样一处理，就和平时的题目类似了。具体过程见下图。

其实，在得到两个根式之差后，除了上图中的平方法，还可以用换元法，也可以直接把处理后的方程与原方程组成一个方程组进行求解。分子有理化也是解双根式方程的一种重要方法，包括前面那个基础题也可以使用，有兴趣的同学可以自己做一下。

此题的难度其实并不大，但是正确率却并不高。一是方程右边出现了x，二是解出的x有两个值，需要验证。如果是你，你做对了吗？

文章来源：《应用数学学报》 网址: http://www.yysxxbzz.cn/zonghexinwen/2021/0426/617.html