大家好，今天和大家分享一道印度初中数学竞赛题：化简二次根式√111556。据说这道题在当时难住了20万印度考生，不少国内网友只看题目觉得挺简单，可是一动笔计算却不得不感叹：确实是太难了。

下面我们一起来看一下这道题：

这是一道求大数的算术平方根的题目。

我们知道，要将一个数开平方，也就是要找到另外一个数的平方等于这个数。对于一些简单的数我们可以一眼看出来，比如169的算术平方根是13，比如961的算术平方根是31等。但是如果一个数比较大，比如2592要进行化简，那么又应该怎么做呢？

对于大数开平方，我们可以先尝试用短除法，将这个大数分解质因数，然后再开方。比如2592可以用短除法进行如下分解：2592=2^5×3^4=6^4×2，所以√2592=36√2。

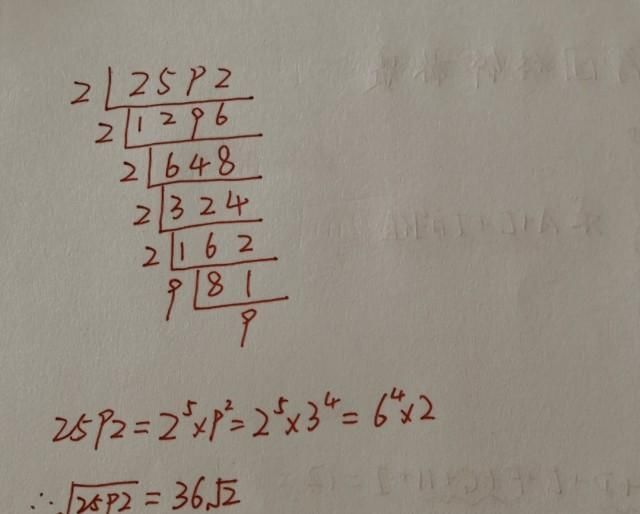
我们先尝试用同样的方法将√111556进行化简。但是我们再用短除法除了2次后会发现，后面就很难找到它的质因数了，计算陷入了困境，所以这个方法在这道题中并不适用了，过程见下图。

那么这道题该怎么解呢？下面介绍两种方法。

解法一：万能解法。

第一步：将被开方数从个位开始每两位数为一组，用“，”隔开，如本题可分为11,15,56；

第二步：先对最左边的这组数开方，开不尽时取最接近的小一点的平方数，开出来的这个数作为商。如本题最左边一组数为11，开出来的数为3；

第三步：用最左边的那组数减去商的平方数，然后在所得的差的后边写上第二组数作为余数，如本题为215；

第四步：用第三步得到的余数作为被除数，把第二步得到的商乘以20，再加上某个数作为除数，但是注意的是加上的这个数与这一步得到的商要相等。比如本题60加3，得到的商也为3；

第五步：重复第三、四步的步骤，但是需要注意的是此时的除数是第二步和第四步这两步得到的数乘以20再加一个数。比如本题660加4；

后面依次重复上面的步骤，直到余数为0。具体过程如下。

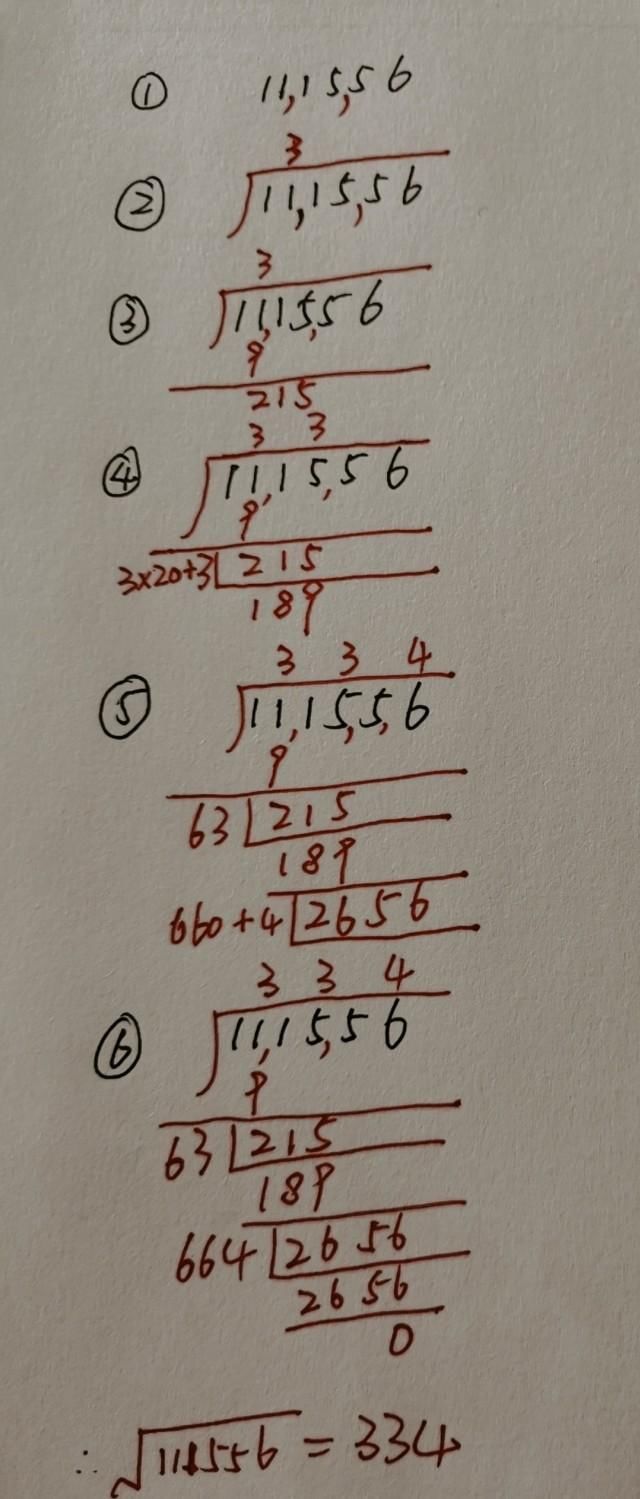
这个方法可以对任意一个数进行开方，对于开不尽的数也可以按要求进行精确计算。大家也可以随便写一个大数试一下，然后用计算器验证。

解法二：巧解。

下面再来看一个巧解的方法。

在初中的简便计算中，经常出现多个1的形式，比如1111。对于这样的形式，我们通常先对这个数字进行变形，如1111=/9=/9。变形后的计算就会变得更加简单了。

本题中也出现111的形式，那么可不可以也进行相应的变形呢？显然是可以的，111556可以写成111111+444+1的形式，然后再变换成10^n的形式。另外，这样变化还有一个好处，那就是分成了三部分，刚好可以和完全平方公式对应起来。具体过程见下图。

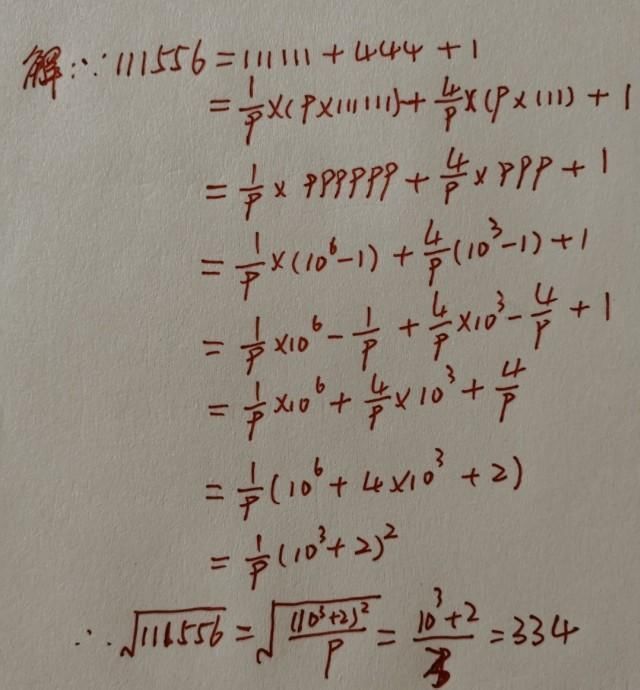
这道印度初中数学竞赛题，据说当时难住了印度20万考生，国内网友也表示真的难。如果是你，你会做吗？

文章来源：《应用数学学报》 网址: http://www.yysxxbzz.cn/zonghexinwen/2021/0426/616.html